Verbesserungen von Jérôme Urhausen, Email vom 10.02.2014, eingefügt.

documents/GeoTopo/GeoTopo.sublime-project

@@ -3,7 +3,7 @@
 	[
 		{
 			"path": "/home/moose/Downloads/LaTeX-examples/documents/GeoTopo",
-			"file_exclude_patterns": ["*.aux", "*.fdb_latexmk"]
+			"file_exclude_patterns": ["*.aux", "*.fdb_latexmk", "*.out", "*.idx", "*.toc"]
 		}
 	],
 	"settings":

documents/GeoTopo/Kapitel2.tex

@@ -701,7 +701,7 @@ Differenzierbare Mannigfaltigkeiten der Klasse $C^\infty$ werden auch
 
               \input{figures/topology-triangle-to-line.tex}
         \item Tori können simplizial auf Sphären abgebildet werden:
-        
+
             \resizebox{0.9\linewidth}{!}{\input{figures/topology-2.tex}}
     \end{bspenum}
 \end{beispiel}
@@ -792,7 +792,7 @@ Differenzierbare Mannigfaltigkeiten der Klasse $C^\infty$ werden auch
         \item Jeder zusammenhängende Graph $\Gamma$ enthält einen
               Teilbaum $T$, der alle Ecken von $\Gamma$ enthält.%
               \footnote{$T$ wird \enquote{Spannbaum} genannt.}
-        \item Ist $n = a_1(\Gamma) = a_1(T)$, so ist $\chi(\Gamma) = 1 - n$.
+        \item Ist $n = a_1(\Gamma) - a_1(T)$, so ist $\chi(\Gamma) = 1 - n$.
     \end{bemenum}
 \end{bemerkung}
 
@@ -829,7 +829,7 @@ Differenzierbare Mannigfaltigkeiten der Klasse $C^\infty$ werden auch
 \end{figure}
 
 \begin{beweis}
-    $\chi(K) = \chi(\Delta) - \underbrace{\underbrace{(-1)^n}_{n-\text{Simplex}} + \sum_{k=0}^n (-1)^k}_{(1+(-1))^{n+1}} = \chi(\Delta) \qed$
+    $\chi(K) = \chi(\Delta) - \underbrace{\underbrace{(-1)^n}_{n\text{-Simplex}} + \sum_{k=0}^n (-1)^k \binom{n+1}{k}}_{(1+(-1))^{n+1}} = \chi(\Delta) \qed$
 \end{beweis}
 
 \begin{satz}[Eulersche Polyederformel]\xindex{Eulersche Polyederformel}%
@@ -844,7 +844,7 @@ Differenzierbare Mannigfaltigkeiten der Klasse $C^\infty$ werden auch
     \begin{enumerate}[label=\arabic*)]
         \item Die Aussage ist richtig für den Tetraeder.
         \item \Obda{} sei $0 \in P$ und $P \subseteq \fB_1(0)$. Projeziere
-              $0P$ von $0$ aus auf $\partial \fB_1(0) = S^2$.
+              $\partial P$ von $0$ aus auf $\partial \fB_1(0) = S^2$.
               Erhalte Triangulierung von $S^2$.
         \item Sind $P_1$ und $P_2$ konvexe Polygone und $T_1, T_2$
               die zugehörigen Triangulierungen von $S^2$, so gibt es 
@@ -863,7 +863,7 @@ Differenzierbare Mannigfaltigkeiten der Klasse $C^\infty$ werden auch
 \end{beweis}
 
 \begin{bemerkung}[Der Rand vom Rand ist 0]\label{kor:9.11}
-    Sei $K$ ein \todo{Warum in Klammern?}{(endlicher)} Simplizialkomplex mit Knotenmenge $V$
+    Sei $K$ ein endlicher Simplizialkomplex mit Knotenmenge $V$
     und $<$ eine Totalordnung auf $V$.
 
     Sei $A_n$ die Menge der $n$-Simplizes in $K$, d.~h.
@@ -890,11 +890,23 @@ Differenzierbare Mannigfaltigkeiten der Klasse $C^\infty$ werden auch
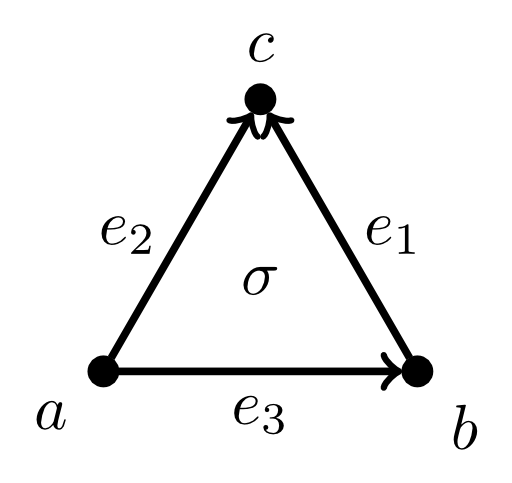
         \caption{Simplizialkomplex mit Totalordnung}
     \end{figure}
 
-    $a < b < c$
+    Sei $a < b < c$. Dann gilt:
 
-    $d_2 \sigma = e_1 - e_2 + e_3 = (c - b) - (c-a) + (b - a) = 0$
+    \begin{align*}
+      d_2 \sigma          &= e_1 - e_2 + e_3\\
+      d_1(e_1- e_2 + e_3) &= (c - b) - (c-a) + (b - a)\\
+                          &= 0
+    \end{align*}
 
-    \todo[inline]{Beispiel auf Tetraeder übertragen}
+    Sei $a<b<c<d$. Dann gilt für Tetraeder:\\
+    \begin{align*}
+      d_3(\Delta(a,b,c,d)) &= \Delta(b,c,d)-\Delta(a,c,d)+\Delta(a,b,d)-\Delta(a,b,c), \text{wobei:}\\
+      d_2(\hphantom{-}\Delta(b,c,d)) &= \hphantom{-}\textcolor{red}{\Delta(c,d)}\textcolor{blue}{-\Delta(b,d)}+\textcolor{green}{\Delta(b,c)}\\
+      d_2(-\Delta(a,c,d))  &= \textcolor{red}{-\Delta(c,d)}+\textcolor{black}{\Delta(a,d)}\textcolor{brown}{-\Delta(a,c)}\\
+      d_2(\hphantom{-}\Delta(a,b,d)) &= \hphantom{-}\textcolor{blue}{\Delta(b,d)}\textcolor{black}{-\Delta(a,d)}+\textcolor{orange}{\Delta(a,b)}\\
+      d_2(-\Delta(a,b,c))  &= \textcolor{green}{-\Delta(b,c)}+\textcolor{brown}{\Delta(a,c)}\textcolor{orange}{-\Delta(a,b)}\\
+      \Rightarrow d_2(d_3(\Delta(a,b,c,d))) &=0
+    \end{align*}
 \end{beispiel}
 
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
@@ -906,7 +918,7 @@ Differenzierbare Mannigfaltigkeiten der Klasse $C^\infty$ werden auch
         d_{n-1}(d_n \sigma) &= d_{n-1} (\sum_{i=0}^n (-1)^i \partial_i \sigma)\\
         &= \sum_{i=0}^n (-1)^i d_{n-1} (\partial_i \sigma)\\
         &= \sum_{i=0}^n (-1)^i \sum_{j=0}^{n-1} \partial_i (\partial_j \sigma) (-1)^j\\
-        &= \sum_{0 \leq i \leq j \leq n-1} (-1)^{i+j} \partial_j (\partial_j (\sigma)) + \sum_{0 \leq j < i \leq n} (-1)^{i+j} \partial_{i-1} (\partial_j \sigma)\\
+        &= \sum_{\mathclap{0 \leq i \leq j \leq n-1}} (-1)^{i+j} \partial_j (\partial_i (\sigma)) + \sum_{\mathclap{0 \leq j < i \leq n}} (-1)^{i+j} \partial_{i-1} (\partial_j \sigma)\\
         &= 0
     \end{align*}
     weil jeder Summand aus der ersten Summe auch in der zweiten

documents/GeoTopo/figures/topology-oriented-triangle.tex

@@ -8,5 +8,5 @@
 
     \draw[->, very thick] (a) edge node[label=below:$e_3$]  {} (b);
     \draw[->, very thick] (b) edge node[label=right:$e_1$]  {} (c);
-    \draw[->, very thick] (c) edge node[label=left:$e_2$]  {} (a);
+    \draw[->, very thick] (a) edge node[label=left:$e_2$]  {} (c);
 \end{tikzpicture}

tikz/topology-oriented-triangle/topology-oriented-triangle.tex

@@ -14,6 +14,6 @@
 
     \draw[->, very thick] (a) edge node[label=below:$e_3$]  {} (b);
     \draw[->, very thick] (b) edge node[label=right:$e_1$]  {} (c);
-    \draw[->, very thick] (c) edge node[label=left:$e_2$]  {} (a);
+    \draw[->, very thick] (a) edge node[label=left:$e_2$]  {} (c);
 \end{tikzpicture}
 \end{document}